Overview
This page discusses a variety of questions concerning math on quantities related to power measurement. Math on certain electrical quantities doesn’t work the way you might expect because some electrical measurements are vector or phasor quantities, so adding or subtracting the amplitudes doesn’t work correctly.
Math with Power Quantities
Can I add the power measured by two different meters together to compute the combined power?
Can I subtract the power measured by two different meters to isolate the power of a particular load or panel?
Yes: real power can be added and subtracted. Although real power can be considered a vector quantity, the phase angle is always the same (zero degrees), so the amplitudes can be added and subtracted.
What about reactive power (VAR)?
Yes: reactive powers can also be added or subtraced from other reactive powers, because again, the phase angle is constant (90 degrees for reactive power). However, it does not make sense to add or subtract reactive powers with real powers.
What about apparent power (VA)?
No: apparent power values cannot be directly added or subtracted from other apparent powers. Apparent power does not have a constant phase angle and different loads may have very different apparent power phase angles and thus cannot be treated as a scalar.
For example, suppose you have two loads, both at 120 VAC and 1.0 amp. One load is purely resistive, while the other is purely capacitive. Both have an apparent power of 120 VA, but when added together, the combined apparent power is 169.7 VA.
You can compute the sum or different of apparent powers, by computing the sum or difference of the real and reactive power values, then using the new real and reactive powers to compute a new apparent power.
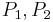 |
Real power |
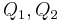 |
Reactive power |
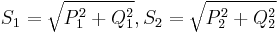 |
Apparent power |
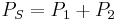 |
Real power sum |
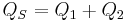 |
Reactive power sum |
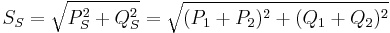 |
Apparent power sum |
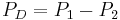 |
Real power difference |
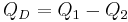 |
Reactive power difference |
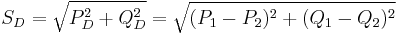 |
Apparent power sum |


