Overview
This article describes the internal measurements and computations used for the WattNode® Pulse meters (WNB series), WattNode BACnet and Modbus meters (WNC series), and WattNode for LonWorks meters (WNC series). The article describes how real energy, power, reactive power, power factor, apparent power, current, and voltage are measured or computed.
Real Energy and Power
The real (or active) energy (kilowatt-hours) is measured for each phase by sampling the voltage and current waveforms 5,000 time per second and multiplying the instantaneous voltage and current values together to calculate instantaneous power, then accumulating or integrating the resulting values to measure energy. Instantaneous power (watts) 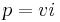 Energy (watt-hours)
Energy (watt-hours) 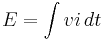 From this, the real or active power is computed as the change in energy per time:
From this, the real or active power is computed as the change in energy per time: 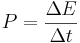 The Pulse WattNode updates the output power (pulse frequency) every 200 milliseconds. The WattNode BACnet and Modbus meters have configurable averaging ranging from 1 second to 60 seconds, while the WattNode for LonWorks updates the power every five seconds. The power and energy measurements include harmonics. However, a harmonic will only contribute to the power and energy as the product of the voltage and current amplitudes. For example, if you are monitoring a load with a strong third harmonic in current, but negligible third harmonic content in the voltage waveform, then there will be negligible real power and energy associated with this third harmonic.
The Pulse WattNode updates the output power (pulse frequency) every 200 milliseconds. The WattNode BACnet and Modbus meters have configurable averaging ranging from 1 second to 60 seconds, while the WattNode for LonWorks updates the power every five seconds. The power and energy measurements include harmonics. However, a harmonic will only contribute to the power and energy as the product of the voltage and current amplitudes. For example, if you are monitoring a load with a strong third harmonic in current, but negligible third harmonic content in the voltage waveform, then there will be negligible real power and energy associated with this third harmonic.
Reactive Energy and Power
Our measurements compute the fundamental reactive power and energy similarly to the real power and energy, but by shifting the current waveform by 90° at the fundamental frequency (generally 50 or 60 Hz). Only the fundamental components of voltage and current are used when computing the reactive power and energy.
Apparent Energy and Power
Only the WattNode BACnet and Modbus meters reports apparent energy and power, although other models compute and use apparent power internally. It is computed as:  Where P is the real power and Q1 is the fundamental reactive power. This equation for computing apparent power is only approximate, because it does not include harmonic reactive power. The preferred equation is
Where P is the real power and Q1 is the fundamental reactive power. This equation for computing apparent power is only approximate, because it does not include harmonic reactive power. The preferred equation is 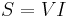 , but the energy measurement IC we use does not provide a direct RMS current measurement.
, but the energy measurement IC we use does not provide a direct RMS current measurement.
Power Factor
We compute the displacement power factor for each phase as:  Because our computed apparent power does not include reactive harmonics, we are measuring the displacement power factor. The average power factor is computed as:
Because our computed apparent power does not include reactive harmonics, we are measuring the displacement power factor. The average power factor is computed as: 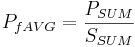
Voltage
The energy measurement chip use in the WNB and WNC series meters measures and reports the RMS voltage for each phase relative to neutral (or ground for delta models).
Estimating Line-to-Line Voltages
The meter chip does not directly measure the phase-to-phase voltage. However, the WattNode BACnet and Modbus meters compute the estimated phase-to-phase voltages for single phase, two and three wire (residential), three phase three and four wire, three phase grounded delta, and three phase four wire (high-leg) delta configurations. See Estimating Line-to-Line Voltages for details.
Current
The energy measurement IC does not provide a current measurement, so WattNode meters estimate the current based on the real and reactive powers and the voltage using the following equation: 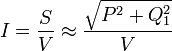 Where S is the apparent power, P is the real power, and Q1 is the fundamental reactive power. Because our reactive power measurement does not include reactive harmonics, the estimated current reported by the WattNode will be low for loads with reactive harmonics. The reported real power and energy will be correct, even if the reported current is low.
Where S is the apparent power, P is the real power, and Q1 is the fundamental reactive power. Because our reactive power measurement does not include reactive harmonics, the estimated current reported by the WattNode will be low for loads with reactive harmonics. The reported real power and energy will be correct, even if the reported current is low.


