Overview
Current transformers (CTs) exhibit two primary errors:
- Accuracy errors (related to gain or linearity)
- Phase angle errors
Accuracy errors are fairly easy to understand. If a CT reads 0.5% low at 20 amps, then it would report 19.9 amps instead of 20 amps. Any measurements based on the current, such as power or energy, would similarly read low by 0.5%.
Phase angle errors are more complex. The current transformer introduces a phase shift (or time delay) in the AC current signal, relative to the actual current. This is commonly measured in degrees and varies from 0.2 degrees (or better) for highly accurate CTs to as high as 6 degrees. At and near unity power factor, CT phase angle errors have little effect on the measured power and energy. However, at lower power factors, such as 0.7 or below (especially below 0.5), even small phase angle errors can cause large errors in the measured power and energy.
WattNode® Compensation
Current transformers traditionally sold by Continental Control Systems, and others vendors, commonly have a leading phase angle error: the current waveform from the CT output leads the actual current. Solid-core or toroid style CTs typically have phase angle errors in the 0.2 degree to 0.5 degree range. Split-core or opening style CTs typically had phase angle errors ranging from 1.0 degree to 2.0 degrees for most models, but as high as 6.0 degrees for the low current CTS-0750-xxx models, such as the 5A, 15A, and 30A. The new Accu-CT® split-core CTs have phase angle errors less than 0.5 degrees, generally less than 0.25 degrees.
We do not calibrate CTs with the WattNode meter, but to reduce the typical phase angle error, we have historically programmed WattNode meters to compensate for a 1.0 degree CT phase angle error. For the toroids, this results in a small overcompensation, but keeps the resulting error less than 1.0 degree. For solid-core CTs, this typically reduces the error from the 1.0 to 2.0 degree range to the 0.0 to 1.0 degree range. For the CTS-0750-xxx models with the higher phase angle errors, the 1.0 degree compensation only somewhat mitigates the larger phase angle error.
Beginning in 2012, with the introduction of the Accu-CT® family of CTs, which have a near zero phase angle error, the default value of the phase angle error correction programmed into WattNode meters was changed from one degree to zero degrees.
Details
Lagging Current – Motor or Inductor Load
In this case, the CT phase angle error (assuming it is greater than one degree) will make the power factor and real power values look higher than they actually are, especially for low power factors. The corrected values will show a lower power factor and lower real power. The energy will show the same error as the power, so if the power reads 2.5% high, then the energy reading will also be 2.5% high.
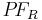 |
Reported (measured) power factor |
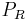 |
Reported (measured) real power |
 |
CT phase angle error (leading, degrees) |
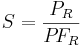 |
Apparent power (not affected by CT phase angle errors) |
 |
Phase angle between line voltage and current (lagging, degrees), based on reported PF |
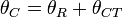 |
Phase angle between line voltage and current with the CT phase error (lagging, degrees). |
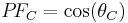 |
Corrected power factor |
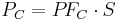 |
Corrected real power |
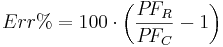 |
Percentage error in reported power |
Example
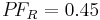 |
Reported power factor |
 |
Reported real power |
 |
CT phase angle error (leading, degrees) |
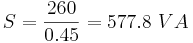 |
Apparent power (not affected by CT phase angle errors) |
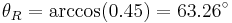 |
Phase angle between line voltage and current (lagging, degrees), based on reported PF |
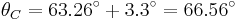 |
Phase angle between line voltage and current with the CT phase error (lagging, degrees). |
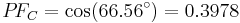 |
Corrected power factor |
 |
Corrected real power |
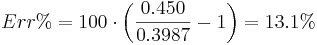 |
Percentage error in reported power |
Leading Current – Capacitive Load
This is less common, but sometimes occurs with power supplies or due to the filter capacitors on inverters. The equations are very similar to the inductive case, but with some signs changed.
In this case, the CT phase angle error (assuming it is greater than one degree) will make the power factor and real power values look lower than they actually are, especially for low power factors. The corrected values will show a higher power factor and higher real power. The energy will show the same error as the power, so if the power reads 2.5% high, then the energy reading will also be 2.5% high.
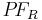 |
Reported power factor |
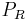 |
Reported real power |
 |
CT phase angle error (leading, degrees) |
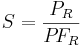 |
Apparent power (not affected by CT phase angle errors) |
 |
Phase angle between line voltage and current (leading, degrees), based on reported PF |
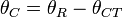 |
Corrected phase angle between line voltage and current (lagging, degrees). |
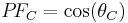 |
Corrected power factor |
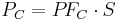 |
Corrected real power |
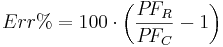 |
Percentage error in reported power |

