What is the difference between “total power factor” and “average power factor”? In 2011, we changed the algorithm for computing the power factor for all phases. At the same time, we changed some of the terminology in our manuals to reflect this change. Originally, we computed the average power factor as the numerical average of the power factors for each phase.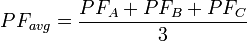 
Inactive phases (line Vac below 20% of nominal) were not included in the computation. However, this has a problem. Suppose phase A is measuring two watts with a power factor of 0.2 (some standby load) while phases B and C are measuring two thousand watts each with a power factor of 0.95. It doesn’t make sense to average the power factor values all together to get a value of 0.7. Given that the equation for power factor for a single phase is the following: 
Where P is the real power and S is the apparent power. It makes more sense to use the same equation when computing the power factor for all phases. 
For our previous example, this would yield the following: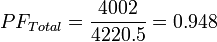 
Reflecting the fact that the two watts on phase A are negligible. The term “power factor average” implies averaging the power factor for each phase together, which is no longer the approach we use. “Power factor sum” might imply adding the power factors for each phase together, possibly yielding numbers greater than 1.0. So we settled on “power factor total” to describe the new computation (although “total” and “sum” have similar meanings). In some cases, to avoid breaking compatibility, we have kept variable names unchanged, like nvoPfAvg for our LonWorks models, but the user manual now uses the term “power factor total” and documents the new computation.
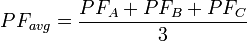Inactive phases (line Vac below 20% of nominal) were not included in the computation. However, this has a problem. Suppose phase A is measuring two watts with a power factor of 0.2 (some standby load) while phases B and C are measuring two thousand watts each with a power factor of 0.95. It doesn’t make sense to average the power factor values all together to get a value of 0.7. Given that the equation for power factor for a single phase is the following: Where P is the real power and S is the apparent power. It makes more sense to use the same equation when computing the power factor for all phases. For our previous example, this would yield the following: 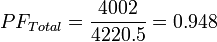Reflecting the fact that the two watts on phase A are negligible. The term “power factor average” implies averaging the power factor for each phase together, which is no longer the approach we use. “Power factor sum” might imply adding the power factors for each phase together, possibly yielding numbers greater than 1.0. So we settled on “power factor total” to describe the new computation (although “total” and “sum” have similar meanings). In some cases, to avoid breaking compatibility, we have kept variable names unchanged, like nvoPfAvg for our LonWorks models, but the user manual now uses the term “power factor total” and documents the new computation.